Kirchhoff’s current law (KCL) is the fundamental law applied to solving various electronic circuits. The German physicist Gustav Robert Kirchhoff defined the KCL.
The KCL is related to the current at the junctions or nodes of an electric circuit. This law states that the algebraic sum of all the current entering or leaving the node must be equal to zero. In other words, we can also say total current entering the circuit is equal to the current leaving the circuit. That’s why Kirchhoff’s current law is also known as the law of conservation of charges.
In this article, we’ll discuss Kirchhoff’s current law in detail and will also solve different examples.
Kirchhoff’s Law
You will encounter several circuits with various component combinations when learning about and understanding circuits.
An electronic circuit is a combination of different electronic components that perform specific tasks.
We encounter various complex electronic circuits, and solving and simplifying those circuits is not possible by using a parallel or series combination simplifying process.
To solve such complex circuits, German physicist Guster Robert Kirchhoff gave two laws which are known as Kirchhoff’s laws. One is Kirchhoff’s voltage law (KVL) and the other is Kirchhoff’s current law (KCL).
Kirchhoff’s voltage law is already discussed, now let’s study Kirchhoff’s current law.
Kirchhoff’s current law (KCL)
Kirchhoff’s current law is also written as KCL. It is one of the fundamental laws in electronic circuit analysis.
KCL is used to analyze and understand electric current behavior in a circuit.
KCL is the law of node or junction. The node is the place in the circuit where two or more elements are connected together.
The KCL states that:
The total current entering a junction or node in a circuit must be equal to the total current leaving that junction or node.
It is also called the law of conservation of charges as the current enters the nodes the same amount of current is leaving the nodes.
Let’s discuss daily life examples to understand KCL.
Suppose you have a pipe that is split into two branches, then these branches are merged into a single pipe.
Assume that water enters the pipe and splits into the two branches. The water from the two branches eventually reunites and exits the junction where they merge.
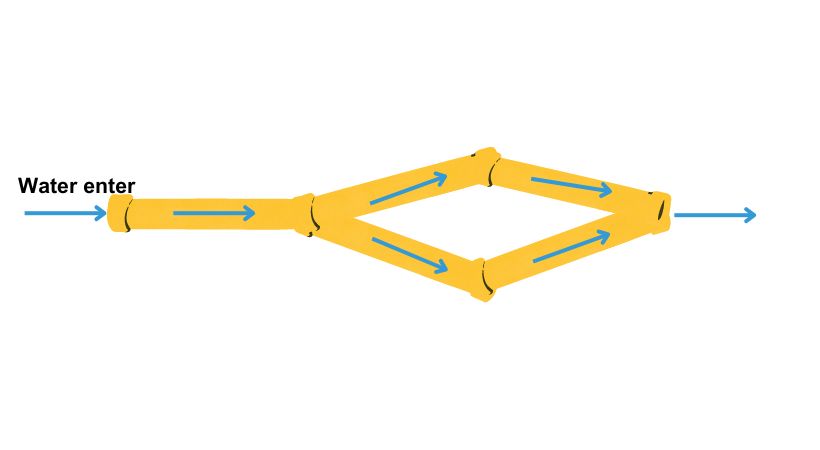
Hence, the amount of water entering the junction equals the amount of water leaving the junction.
In an electronic circuit, you can think of electric currents as the flow of water, and the junctions or nodes as the points where the currents split or merge.
KCL tells us that the algebraic sum of currents entering a node or junction must be equal to the sum of currents leaving that node or junction.
Mathematically, it is given by
∑I_IN=∑I_Out
The sign convention for KCL is important to learn before discussing examples.
In convention the currents entering the junction are given a positive sign and currents leaving the junction are given a negative sign. This ensures that the current at the node is equal to zero.

Like in the above circuit, we have one node I_1, I_2, and I_3 entering into the node so a positive should be signed to it, and I_4, I_5 is leaving the node so a negative sign should be given.
I_1 + I_2 + I_3 + (-I_4) + (-I_5)=0
I_1 + I_2 + I_3 = I_4 + I_5
∑I_IN=∑I_Out
As the equation shows the sum of the currents entering the node is equal to the currents leaving the node.
Examples
Here is an example to learn how can you find current and voltage in a circuit using KCL. Find the node voltage and current through the resistors using KCL.
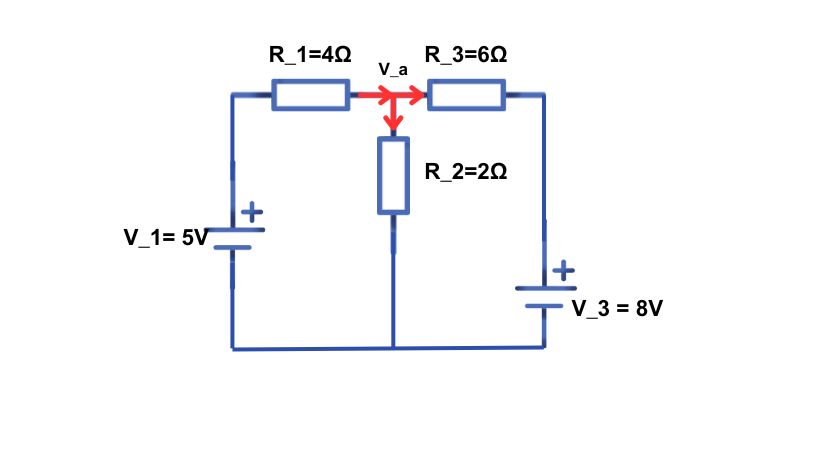
In the above circuit, we have three resistors, two voltage sources, and one node V_a. As you can see the current I_1 is entering the node V_a and the current I_2 and I_3 leaving the node V_a.
Applying KCL on node V_a
I_1 + (-I_2) + (-I_3) = 0 ………. (1)
I_1 – I_2 – I_3=0
According to Ohm’s law
I=V/R
So equation one becomes
(5-V_a/R_1) – (V_a – 0/R_2) – (V_a – 8/R_3)=0
(5 – V_a/4Ω) – (V_a – 0/2Ω) – (V_a – 8/6Ω) = 0
(15 – 3V_a – 6V_a – 2V_a + 16/12)=0
-11V_a = -15-16
-11V_a = -31
V_a = -31/-(11)
V_a = 2.818V
Now we can find the values of the different currents flowing in the node.
I_1 = 5 – V_a/R_1
I_1 = 5-2.81/4
I_1 = 0.54A
Current through resistor R2
I_2 = V_a – 0/R_2
I_2 = 2.81/2
I_2 = 1.405A
For R3
I_3 = V_a – 8/R_3
I_3 = 2.81-8/6
I_3 = -0.865A
To verify KCL, as we know the current entering node must be equal to the leaving currents. From equation (1)
I_1 – I_2 – I_3=0
I_1 = I_2 + I_3
0.54 = 1.405-0.865
0.54A = 0.54A
This is how we analyze circuits with the help of KCL.
Significance of Kirchhoff’s current law
KCL is a fundamental law of electronic circuits, and its significance cannot be overstated. Here are a few reasons why it is crucial in circuit analysis:
- KCL, along with Kirchhoff’s Voltage Law (KVL), forms the foundation for analyzing electronic circuits.
- Circuits can become quite complex, so KCL provides a systematic way to analyze these circuits, breaking them down into simpler, solvable equations.
- KCL is extensively used in network theorems like Thevenin’s and Norton’s theorems, as well as in techniques such as Mesh Analysis and Nodal Analysis.
- Help in solving large-scale circuits and networks, whether in power distribution, communication systems, or integrated circuits.
To understand basic electronics and circuit connections, learning Kirchhoff’s current law is essential. Make sure to understand it and practice on different circuits.
Conclusion
To analyze the electronic circuits different laws and rules are used. Some circuits are straightforward and Ohm’s law can simplify them but at an advanced level, the circuits become complicated.
Kirchhoff’s law will be used to solve or study the behavior of these complicated or complex circuits. The KVL and KCL are the two laws.
The KCL states that the algebraic sum of current entering the node or junction will equal the current leaving the junction or node. The node or junction is the place in the circuit where two or more components connect.
The current entering the node should be taken positive and the current leaving the node should be taken negative.
Thank you and this was all about KCL…
Other useful posts:
