The electronic circuit has both series and parallel combinations, these types of circuits can be simplified with Ohm’s law but if the circuit has more than one voltage source simple Ohm’s law can’t be helpful.
German physicist Gustav Robert Kirchhoff significantly contributed to the understanding of electronic circuits. Kirchhoff’s voltage law (KVL) refers to the voltage drop in a closed circuit or closed loop. In KVL the algebraic sum of all the voltage drops in the closed loop equals zero. The KVL statement is the law of conservation of energy.
This article will discuss the KVL in detail with proper examples for your understanding.
Kirchhoff’s voltage law (KVL)
Electronic circuits are the composition of various components that are connected to perform specific tasks.
When learning and understanding circuits you come across different circuits that have different component combinations.
Parallel and series combinations are the types of circuits in which components can be connected.
When components are connected in line and have a single path for the current to flow, the combination is called a series circuit.
If the components are arranged in such a way that there are multiple pathways for the flow of current, the circuit is a parallel circuit.
The parallel and series circuit can be simplified by Ohm’s law easily.
However, sometimes we encounter circuits, where simplification by series and parallel combination is impossible. Here, Ohm’s cannot be applied to simplify these circuits.
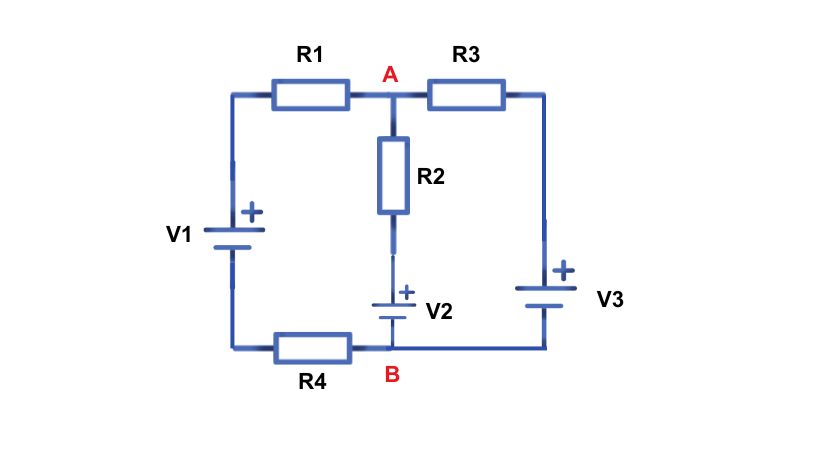
This happens when the circuit has more than one voltage source and electronic components are connected in a complex manner, which means it can’t be identified if they are connected in series or parallel.
For example, in the above circuit, we have three voltage sources V_1, V_2, V_3, and four resistors R_1, R_2, R_3, and, R_4. Looking at their connections, we can’t say if they are in parallel or series.
Between points A and B in the circuit, there is a resistor and voltage, which makes solving this circuit difficult.
German physicist Gustav Robert Kirchhoff devised two laws to solve such complex circuits, one known as Kirchhoff’s Voltage law.
KVL is the fundamental law used for analyzing circuits. In KVL we considered loops and simplified the circuit.
A loop is a closed conducting path in a circuit that encounters no node more than once and is also called mesh.
Kirchhoff’s voltage law is also known as mesh analysis.
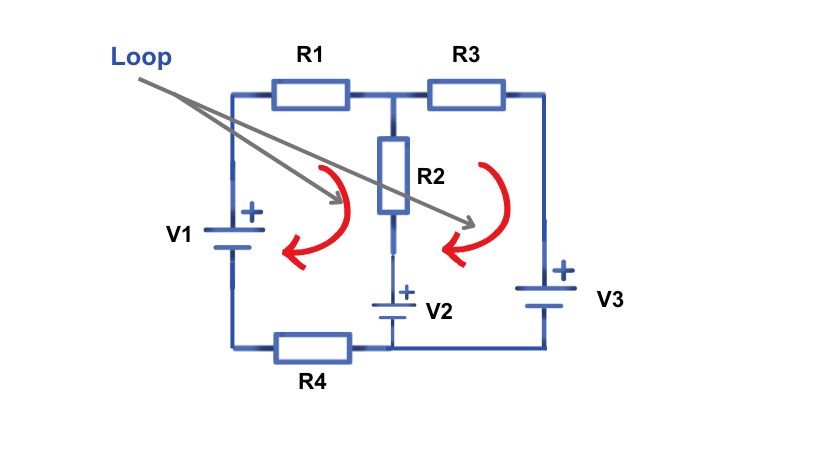
The KVL states that:
In any closed-loop circuit, the algebraic sum of all the voltage sources and voltage drops in components is equal to zero or the sum of the potential difference around the loop must be equal to zero.
Algebraic sum of potential difference + Algebraic sum of voltage drop = 0
Let’s consider an example to understand the KVL more. The given circuit has a single loop.
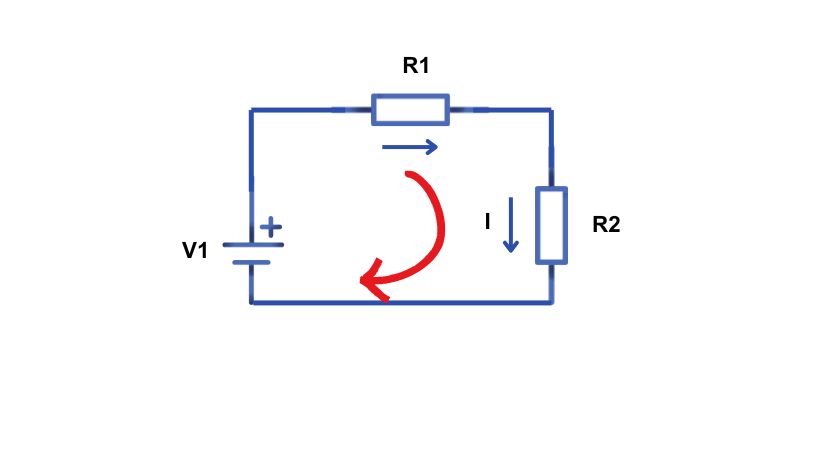
Starting from any point in this closed circuit, let’s say start from V_1 and go back to this point after going around the circuit, then there is no increase and decrease in the potential difference.
Due to this KVL is also referred to as the law of conservation of energy.
As you move in the closed circuit, you will end back to the position from where you started with no loss of voltage across voltage.
It is essential to pay attention to the signs (+ or -) of the voltage source and drop across the components. Otherwise, you will get the wrong results.
So consider single components such as a resistor to understand the voltage drop across the components.

As the current flows from the positive terminal (A) to the negative terminal (B), this is the conventional flow of current. In this situation, there will be a fall in the voltage across the resistor and give -IR voltage drop across it.
However, if the current is flowing from B to A, there will be a rise in the potential across the resistor, as we are moving from a – potential to a + potential giving us a +IR voltage drop.
When applying KVL some rules should be considered.
- The positive sign should be taken if there is a rise in the potential.
- A voltage drop across any component should be taken negative.
- For voltage sources, the positive terminal is always at a higher potential.
- Current flow from high potential to the lower potential means from positive to negative terminal.
- Assume the flow current is either clockwise or counterclockwise.
All these rules are followed for examples which are discussed in this article.
Examples
Let’s understand Kirchhoff’s voltage law (KVL) through different circuit examples.
Example no. 1
Let’s consider a single-loop circuit and verify the KVL.
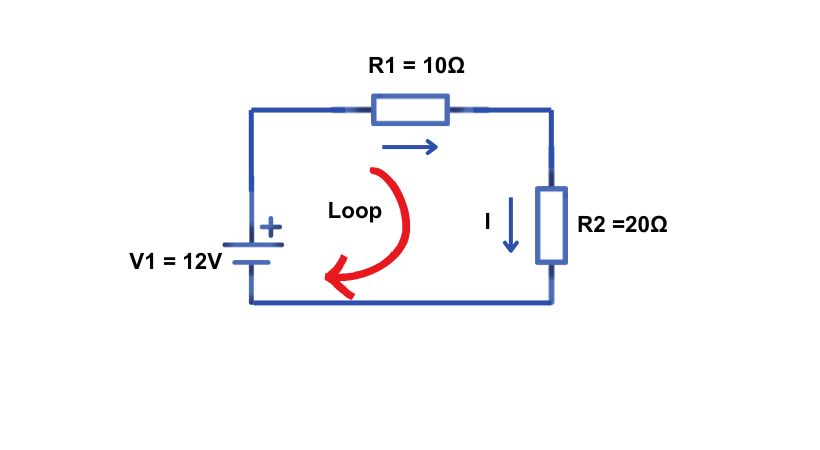
As KVL says the algebraic sum of all the applied voltage and drops is equal to zero. The loop started with applied voltage and ended on it.
The resistors are connected in series so the same current is flowing.
V_1 + (-IR_1) + (-IR_2)=0
The applied voltage VS is positive and the voltage drops across R1 and R2 is taken negative. The above equation can also be written as
V_1 = IR_1 + IR_2
Current can be taken as common because resistors have a series combination and the same current is flowing in both.
V_1 = I(R_1 + R_2)
Where
R_T = R_1 + R_2
As R_1 = 10Ω and R_2 = 20Ω so
R_T = 10Ω+20Ω
R_T=30Ω
V_1=I*R_T
The current from the above equation is equal to
I = V_1/R_T
I = 12V/30Ω
I = 0.4A
As the current same on both resistors, the voltage drop is given by
V_R1 = I*R_1
V_R1 = 0.410V
V_R1 = 4V
For resistor R2
V_R2 = I*R_2
V_R2 = 0.420
V_R2=8V
Now we can verify the Kirchhoff’s voltage law
V_1+(-IR1)+(-IR2)=0
Let’s put the values of voltage drops and applied voltage.
12V+(-4V)+(-8V)=0
12-4V-8V=0
Thus Kirchhoff’s voltage law is true, as the individual voltage drops and applied voltage around the closed loop is equal to zero.
Example no. 2
Find the current through all the resistors using Kirchhoff’s voltage law (KVL).
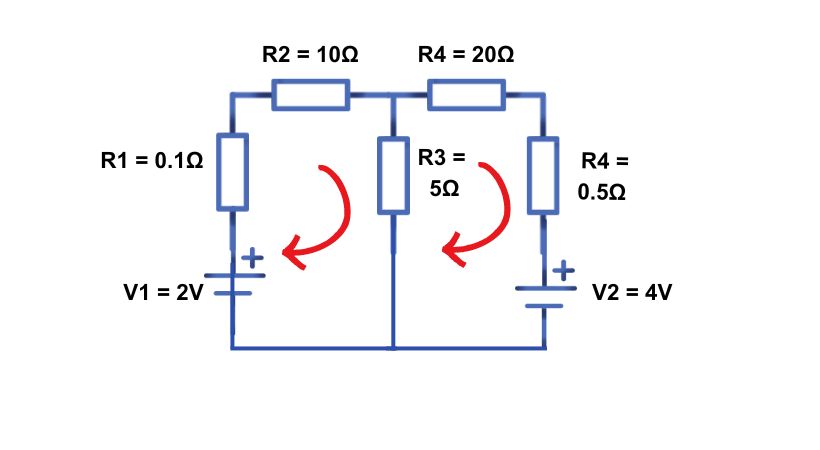
For Loop 1
V_1-(I_1*R_1)-(I_1*R_2)-[(I_1*R_3)+(I_2*R_3)] = 0
The V_1 is taken positively because the current is flowing from positive to negative and all the drop is negative. In the resistor, R_3 the current I_2 is also flowing so it will be added.
Now put the values of resistors and applied voltage in the above equation.
2V-(0.1*I_1) – (10*I_1)-(5*I_1) + (5*I_2) = 0
2V-(15.1*I_1) + (5*I_2) = 0
(-15.1*I_1 + 5*I_2)=-2 …………………. (1)
For loop 2
(-I_2*R_5) – V2 – (I_2*R_3) + (I_1*R_3) – (I_2*R_4) = 0
Now put the values of resistors and applied voltage in the above equation.
(-0.2*I_2) – 4 – (5*I_2) + (5*I_1) – (20*I_2) = 0
-4- (25.2*I_2) + (5*I_1) = 0
(5*I_1) – (25.2*I_2) = -4 ……………. (2)
To find the value of current I_1 and I_2 Using equation (1)
(-15.1*I_1) + (5*I_2) = -2
(-15.1*I_1) = -2-(5*I_2)
I_1 = -2 – 5I_2/-15.1 ………..(3)
Now put equation (3) in eq (2)
(5*I_1) – (25.2*I_2) = -4
5(-2-5I_2/-15.1)-(25.2*I_2) = -4
(-10-(25I_2)/-15.1)-25.2*I_2 = -4
(-10/-15.1-25I_2/-15.1)-25.2*I_2 = -4
0.66+(1.6688I_2) – (25.2I_2) = -4
(1.6688*I_2) – (25.2*I_2) = -4-0.66
-23.5312*I_2= 3.34
I_2= 3.34/-23.5312
I_2= -0.1419A …….. (4)
Put eq (4) in either eq (1) or eq (2)
-15.1*I_1 + 5*I_2=-2
-15.1*I_1 + 5(-0.1419) = -2
-15.1*I_1 – 0.7095 = -2
-15.1*I_1 = -2+0.7095
I_1 = -1.2905/-15.1
I_1 = 0.085A
The values of the current are known this will help you to find the current and voltage in each resistor. Let’s calculate the current and voltage in R_3
As we know R_3 both currents are flowing so using eq (1) we have
I_R3= -I_2 + I_1
By rearranging the above equation
I_R3 = (I_1 – I_2)
Now put the values
I_R3 = (0.085-(-0.1419))
I_R3 = 0.2269A
By using the current you can also find voltage through R_3
V_R3 = I_R3*R_3
V_R3 = 0.22695
V_R3 = 1.1345V
In the same way, you can find the voltages in other resistors. Find the current and voltage in other resistors for your practice.
Common mistakes in applying KVL
Highlighting typical mistakes helps beginners apply KVL correctly:
- Students mistakenly apply the wrong signs for voltage drops or gains, leading to wrong results.
- Forgetting to account for all components, such as resistors or voltage sources, can lead to incomplete equations.
- Switching directions in the middle of a loop when tracing it can result in incorrect summation of voltages.
Conclusion
Kirchhoff’s laws are fundamental in electronic circuits to solve the circuits and find current and voltage across various components.
Kirchhoff’s voltage law (KVL) and Kirchhoff’s current law (KCL) are two laws represented by German physicist Gustav Kirchhoff.
When the components are connected in a very complicated manner and have more than one voltage source then Kirchhoff’s laws are essential.
Kirchhoff’s voltage law (KVL) states that the algebraic sum of all the applied voltage and voltage drop across the resistor in the closed loop is equal to zero.
A loop, also known as a mesh, is a closed conducting channel in a circuit that never comes into contact with a node more than once.
The direction and polarity of current and voltage are important to consider while solving the circuit using KVL, otherwise, it will give you wrong results.
This was all about KVL, I hope the provided information and examples help you to solve various circuits.
Thank you…
Other useful posts:
